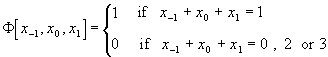Symbolic dynamics and codes

Genesis 

Dynamical systems appeared at the beginning of XVIII century following the Newton’s description of dynamics in physics. The motion is governed by a system of differential equations. The typical example here is the motion of the solar system, where the equilibrium between gravity and centrifugal force is attained. This discovery triggered a rapid development of methods of solving differential equations which became the main subject of mathematics for almost two centuries. The names of Euler or Jacobi must be mentioned here. In some cases explicit motion equations have been found, like in the case of two celestial bodies (Newton himself). Powerful tools like complex analysis and Fourier analysis have been developed to deal with more and more difficult differential equations.

Nevertheless, finding explicit motion equations turned out impossible except for only very few elementary cases. This difficulty challenged mathematicians and physicists at the end of the XIXth century to try a more abstract approach, i.e. to search for answers to some questions concerning the motion without knowing the explicit equation. The best examples of such results are the Poincaré recurrence theorem and the Ergodic Theorems by Birkhoff and von Neumann. No wonder that these very abstract theorems (nowadays known and quoted to in their modern abstract formulations) have been first proved only for smooth dynamical systems in the Euclidean space or on a Riemannian manifold.

One of the typical subjects investigated by that time was describing geodesic curves on a Riemannian manifold. Such curves are solutions to certain differential equations for minimizing length of a path joining given points on the manifold and they appear naturally as trajectories of moving particles.

Reviewing Journal de Mathématiques of 1898 we can find works by Poincaré, Laurent, Liapunov, Jordan and the like. On of them is Hadamard’s paper concerning geodesics on Riemannian manifolds with negative curvature.

We are used to think about symbolic dynamics as of investigating binary sequences, blocks and codes, which has more to do with information theory rather than classical description of smooth motion. But it is the XIXth century paper by Hadamard where the origins of symbolic dynamics can be found. Let’s take a closer look.

Hadamard considers homotopy classes of curves. He proves that there exists a finite set of closed curves G={g₁, g₂, ... ,g_n}, such that each class represents traversing these curves in a particular order, in other words  it  is described by a double  infinite sequence  A = ...  a_-1, a₀, a₁,...  (a_i ÎG). Next he proves that every class contains exactly one geodesic. By a certain additional assumption on the shape of the manifold this establishes a 1-1 correspondence between all bounded geodesics and all double infinite sequence over the alphabet G. For a detailed explanation of Hadamard’s idea we shall use the simplest manifold of negative curvature with nontrivial set of geodesics. Below is a computer generated picture of such a manifold. We can distinguish three regions which we call saddles and components extending to infinity which we call cones. Suppose we start drawing a geodesic from a saddle. We are free to choose the initial direction within the range of 180°. If we choose a direction going to much left or right then the geodesic will climb one of the cones and escape to infinity. The same holds for central directions. Thus we are left with two intervals of directions I₁ and I₂ going toward two remaining saddles. The saddles are sensitive to small changes of directions, i.e. changing the initial direction within the interval I₁ we can obtain the full range of 180° on the second saddle. Again, the extreme and middle directions escape to infinity, hence from I₁ we select only two smaller subintervals. The same holds for I₂. And so on. It is now seen that the set of initial directions which do not escape is a classical Cantor set, and since we have two choices on each saddle (left and right), every such geodesic can be coded by an infinite sequence over two symbols {l , r}.  In fact, there are two Hadamard’s basic closed curves for this manifold.

  Hadamard’s idea was exploited in the years 1920-21 by an American mathematician Harold Marston Morse. By that time the concept of a minimal flow was already known along with the uniform recurrence criterion, still an example of a nonperiodic minimal flow was missing. At first, Morse proved that Hadamard’s coding is continuous (i.e. two sequences are equal on a long centered interval if and only if the corresponding geodesics are close to each other along a long interval). Then he proved that periodic sequences correspond to closed geodesics. Using the modern language, Morse has shown that the geodesic flow (observed along integer time moments) contains the full symbolic shift (G^Z,S) as a subflow. Finally, he and a Norwegian Thue constructed the famous example of a minimal nonperiodic sequence known today as the Thue-Morse sequence. This sequence is obtained inductively by starting with a zero and then, in consecutive steps, by adding the negative of what was constructed so far.

0-1-10 -1001-10010110-1001011010011001-...  

What is important, Morse introduced a completely new abstract approach to the subject. He was able to get rid of differential equations and use combinatorial tools such as blocks, patterns, codes, and substitutions. This is why Morse is being called the discoverer of the modern symbolic dynamics. By that time however he has not yet realized the real value of his novelty. In his paper the nonperiodic minimal flow is still interpreted as a certain geodesic. But in 1938 with cooperation with Gustav Arnold Hedlund he writes a paper entitled „Symbolic Dynamics” fully devoted to abstract symbolic systems. In the textbook „Topological Dynamics” by Gottshalk and Hedlund (1955) the investigation of symbolic dynamics constitutes a separate chapter. It is already known that symbolic flows are characterized by two basic properties: zero-dimensionality and expansiveness.

Cellular automata

Currently symbolic dynamics has grown to a large area of investigation. It includes new fields such as the theory of cellular automata, information theory, theory of error correcting codes and other applied topics. Let me explain the idea of a block code. It was proved by Hedlund already in 1969 that every factor map j  from one symbolic flow (X,S) to another (Y,S) must be generated by a mapping F: S^2r+1®S, (the parameter r is called the radius of the code) by the formula:

j(x)(i) = F(x[i-r, i+r]).

The theory of such codes (called cellular automata) was introduced in the forties by von Neumann and Ulam. But its meaning increases after 1969. Hedlund formulated several conditions for the map j  generated by the code to be surjective with respect to the full shift (S^Z,S). Analogous criteria for subshifts are currently a subject of research. Similarly, the dynamics of such maps are being investigated. Let us mention the results by Gilman (1987) where classification of codes with respect to properties such as expansiveness, sensitivity and equicontinuity is given, and by Hurley (1990) where codes are classified by the size and quantity of attractors. Finally, P. Kůrka (1994) investigates intersections of classes arising from the two above classifications.

For example, let us consider a code over two symbols {0, 1}:

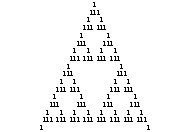
Below is we see consecutive images by iterating this code starting from the sequence containing all zeros except a single digit 1 (zeros are replaced by dashes).

What we see resembles the famous Sierpinski triangle. The picture becomes even more complicated if we start with a randomly chosen 0-1 sequence:

As mentioned above, not much is known about the dynamics of such codes in the general case.
There is an interesting story connected to such codes. Scientist investigating genetics of sea snails were interested in finding out mechanisms responsible for the patterns appearing on the shells of certain species.

It is well known that the shells grow along one edge by building up one row of cells each period of time. Designs like these will appear when some of the cells will contain pigment and other not. It was assumed by the biologists that the design of the whole pattern is encoded genetically and passed from one generation to another. Next there should exist a mechanism allowing to realize the pattern by controlling the pigmentation of each cell during the snail’s entire life according to the global genetic plan. They were expecting to find some kind of a hormone carrying the information individually to each new growing cell. But soon it turned out that such hormone does not exist. All hormones are spread evenly along the edge of the shell, so only horizontal straps as on the next picture can be produced by this method. The solutions was found only after consulting the subject with specialists working with codes and automata. They recognized that the pattern must follow simple block codes, in most cases of radius 1. We can compare the shells with iterates of appropriately selected block codes.  

Thus, it became clear that there is no global design stored in the genes. The pattern on the shell appears automatically. The new built cell is filled with pigment or not depending on the pigmentation of three neighboring old cells. A simple chemical mechanism suffices to realize such dependence. Of course, the question why snails need these patterns remains open, but this belongs to a different area of science.

Another example leading to an application of block codes is the so called ”firing squad problem”. The code can be interpreted as a system of communication between soldiers in which each soldier in the squad receives signals from his two neighbors (or one if the soldier occupies one of the extreme positions in the squad). The code should lead to simultaneous firing of all soldiers and it should not depend on the number of soldiers, i.e. the same code should work with squads of different sizes. There exist many solutions to this assignment which is often used as an exercise at programming courses. But it also has a more practical application. Namely it can be used  in computer networks to synchronize certain actions of all elements of a net, the number of which is a priori unknown. This example can give us an idea how useful symbolic dynamics can be. Most sophisticated methods of theoretical research often combined with numerical investigation find direct application in advanced technology via information theory, theory of error correcting  codes, neural networks designing or genetic codes. Let me only mention the obvious fact that receiving satellite TV broadcasting would not be possible without codes.