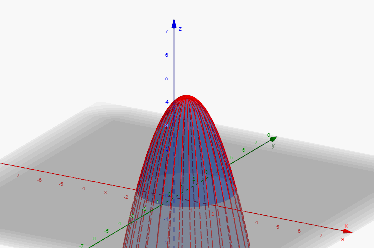
Przykład 1
Funkcja ma w punkcie maksimum lokalne właściwe równe . Rzeczywiście, dla każdego różnego od zachodzi oczywista nierówność
Ilustruje to rysunek poniżej.
Definicja 1
Załóżmy, że funkcja dwóch zmiennych jest określona w pewnym obszarze .
Mówimy, że:
ma maksimum lokalne właściwe w punkcie
jeżeli istnieje takie otoczenie kołowe
punktu
że dla każdego
różnego od
zachodzi
nierówność
ma minimum lokalne właściwe w punkcie
jeżeli istnieje takie otoczenie kołowe
punktu
że dla każdego
różnego od
zachodzi
nierówność
Jeżeli nierówności i zastąpimy odpowiednio nierównościami i wówczas mówimy, że funkcja ma w punkcie maksimum (odpowiednio: minimum) lokalne niewłaściwe.
Mówimy krótko, że funkcja ma w punkcie ekstremum, jeżeli ma w maksimum lub minimum lokalne (właściwe lub niewłaściwe).
Jeżeli funkcja ma w punkcie ekstremum i to mówimy, że funkcji w tym punkcie jest równe
Przykład 1
Funkcja ma w punkcie maksimum lokalne właściwe równe . Rzeczywiście, dla każdego różnego od zachodzi oczywista nierówność
Ilustruje to rysunek poniżej.

Przykład 2
Funkcja ma w punkcie minimum lokalne właściwe równe zeru. Rzeczywiście, dla każdego różnego od zachodzi nierówność
Przykład 3
Funkcja ma w każdym punkcie postaci gdzie maksimum lokalne niewłaściwe równe .
Rzeczywiście, jeżeli i to w każdym punkcie postaci funkcja przyjmuje wartość
Jeżeli z kolei to
Tak więc w każdym otoczeniu punktu nasza funkcja albo przyjmuje wartość , albo wartość mniejszą od . W myśl definicji funkcja ma więc w punkcie maksimum lokalne niewłaściwe.
Rysunek poniżej ilustruje całą sytuację.

Przykład 4
Rozważmy funkcję Zauważmy, że:
dla każdego zachodzi mamy ;
dla każdego zachodzi mamy
Widzimy więc, że funkcja przyjmuje zarówno wartości mniejsze, jak większe od w dowolnie małym otoczeniu punktu Oznacza to w szczególności (w myśl definicji), że nie ma w punkcie ekstremum. Rysunek poniżej ilustruje zachowanie funkcji w pobliżu punktu

Z rozważań powyżej wynika, że punkt wykresu funkcji ma ciekawą cechę. Mowiąc poglądowo, gdy oddalamy się od niego wzdłuż płaszczyzny – a więc "stąpamy" po punktach postaci – wówczas nasze położenie jest coraz wyższe. Gdy oddalamy się od niego wzdłuż płaszczyzny wówczas nasze położenie jest coraz niższe. Czerwone krzywe na rysunku powyżej pokazują, że pierwsze lub drugie zjawisko zachodzi również w przypadku oddalania się od naszego punktu również wzdłuż innych płaszczyzn pionowych zawierających oś
Warto też zauważyć, że gdy oddalamy się od punktu wzdłuż płaszczyzn oraz to wysokość naszego położenia nie zmienia się: dla każdego zachodzą bowiem równości
Punkt powierzchni o takiej własności, jak opisana powyżej, nosi nazwę punktu siodłowego. Punkty siodłowe powinny być Ci dobrze znane, jeśli uprawiasz turystykę górską – występują one na przełęczach.
Wyznaczanie ekstremów funkcji dwóch zmiennych odbywa się podobną metodą, jak w rachunku różniczkowym funkcji jednej zmiennej. Naciśnij przycisk "Powtórka" poniżej, jeżeli nie pamiętaz lub niedokładnie pamiętasz tę metodę.
Gdy wyznaczaliśmy ekstrema funkcji jednej zmiennej przy pomocy rachunku różniczkowego, to wykorzystywaliśmy następujące twierdzenie.
Jeżeli funkcja ma w punkcie ekstremum i ma w tym punkcie pochodną, to
Powyższe twierdzenie mówi, że ekstremum funkcji jednej zmiennej może wystąpić tylko w takim punkcie, w którym pochodna funkcji jest równa zeru.
W celu wyznaczenia ekstremów obliczaliśmy pochodną funkcji , po czym rozwiązywaliśmy równanie Rozwiązania tego równania nosiły nazwę punktów stacjonarnych funkcji .
Wyznaczenie punktów stacjonarnych pozwalało orzec, że funkcja nie może mieć ekstremum nigdzie poza nimi.
Natomiast stwierdzenie, czy funkcja ma w danym punkcie stacjonarnym ekstremum, czy nie, wymagało zbadania dodatkowych warunków, zwanych warunkami dostatecznymi istnienia ekstremum funkcji. Przypomnijmy dwa takie warunki.
Jeżeli oraz pochodna zmienia znak w punkcie (to znaczy w pewnym przedziale zawierającym przyjmuje po obu stronach punktu wartości przeciwnych znaków), wówczas ma w punkcie :
minimum lokalne, gdy dla oraz dla ();
maksimum lokalne, gdy dla oraz dla ().
Jeżeli funkcja ma w drugą pochodną ciągłą oraz zachodzą jednocześnie warunki
wówczas ma w punkcie :
minimum lokalne, gdy ;
maksimum lokalne, gdy ;
Przykład
Rozważmy funkcję
Pochodna funkcji jest równa
Równość jest spełniona wtedy i tylko wtedy, gdy lub . Są to punky stacjonarne funkcji .
Druga pochodna funkcji jest równa .
Zachodzą nierówności
Wynika stąd, że funkcja ma maksimum w punkcie i minimum w punkcie
Podobnie, jak w przypadku funkcji jednej zmiennej, funkcja dwóch zmiennych może mieć ekstremum tylko w takim punkcie, w którym zerują się obie jej podobne cząstkowe (o ile w tym punkcie istnieją).
Twierdzenie 1 (warunek konieczny ekstremum)
Jeżeli funkcja ma ekstremum lokalne w punkcie i ma w tym punkcie pochodne cząstkowe i to są one obie równe zeru:
Jeżeli to punkt nazywamy punktem stacjonarnym lub krytycznym.
Podobnie jak w przypadku funkcji jednej zmiennej, zerowanie się obu pochodnych cząstkowych funkcji w punkcie nie implikuje istnienia w tym punkcie ekstremum lokalnego.
Przykład 6
Rozważmy funkcję Jej pochodne cząstkowe
są równe zeru w punkcie
Jednak funkcja nie ma w tym punkcie ekstremum lokalnego.
Rzeczywiście, dla każdego i mamy
Jednoczesnie dla każdego i mamy
Tak więc w dowolnie małym otoczeniu punktu funkcja przyjmuje zarówno wartości większe, jak wartości mniejsze od swojej wartości w
Następne twierdzenie podaje warunek dostateczny istnienia ekstremum lokalnego funkcji dwóch zmiennych.
Twierdzenie 2
Załóżmy, że funkcja ma ciągłe pochodne cząstkowe drugiego rzędu w otoczeniu punktu oraz zachodzą warunki:
gdzie
Wówczas funkcja ma w punkcie :
maksimum lokalne właściwe, jeżeli
minimum lokalne właściwe, jeżeli
Jeżeli to funkcja nie ma w punkcie ekstremum lokalnego.
Wyznacznik macierzy złożonej z pochodnych cząstkowych drugiego rzędu funkcji nosi nazwę hesjanu od nazwiska XIX-wiecznego matematyka niemieckiego Ludwiga Otto Hessego.
Uwaga. Ponieważ w powyższym twierdzeniu zakładamy ciągłość pochodnych cząstkowych drugiego rzędu, więc (na mocy twierdzenia Schwartza o równości pochodnych mieszanych) dla każdego punktu w omawianym otoczeniu punktu zachodzi równość Wynika stąd, że
Uwaga. Powyższe twierdzenie nie orzeka istnienia (bądź nieistnienia) ekstremum w przypadku, gdy hesjan jest w punkcie równy zeru. W takim punkcie funkcja może mieć, a może nie mieć ekstremum. Fakt ten trzeba zbadać innymi metodami, na przykład na podstawie definicji ekstremum. Ilustrują to dwa ćwiczenia poniżej.
Zadanie 1
Niech Funkcja ma w punkcie minimum lokale właściwe, ponieważ oraz dla każdego zachodzi nierówność
Sprawdź, że oraz że
Pochodne cząstkowe funkcji są równe
Widzimy, że
Wyznaczamy pochodne cząstkowe drugiego rzędu funkcji :
Zatem
Widzimy, że
Zadanie 2
Niech Funkcja nie ma w punkcie ekstremum. Rzeczywiście, dla dowolnych mamy oraz dla dowolnych mamy Jednocześnie Zatem w dowolnie małym otoczeniu punktu funkcja przyjmuje zarówno wartości większe, jak wartości mniejsze od swojej wartości w
Sprawdź, że – podobnie, jak w poprzednim cwiczeniu –
Pochodne cząstkowe funkcji są równe
Widzimy, że
Wyznaczamy pochodne cząstkowe drugiego rzędu funkcji :
Zatem
Widzimy, że
[Egz] Zadanie 3
Wyznacz ekstrema funkcji
Funkcja nie ma ekstremów.
Obliczamy pochodne cząstkowe:
Widzimy, że jedynym rozwiązaniem układu równań jest punkt
Pochodne cząstkowe drugiego rzędu są równe:
Mamy wobec tego
Ponieważ wyznacznik pochodnych drugiego rzędu jest ujemny (nawet niezależnie od wartości ), więc funkcja nie ma w punkcie ekstremum.
Rysunek poniżej ilustruje całą sytuację.

[Egz] Zadanie 4
Wyznacz ekstrema funkcji
Funkcja ma w punkcie minimum lokalne.
Obliczamy pochodne cząstkowe:
Rozwiązujemy uklad równań
Widzimy, że nasz uklad ma dwa rozwiązania: oraz Są to punkty stacjonarne funkcji Tylko w tych punktach funkcja może mieć ekstrema.
Aby przekonać się, czy funkcja ma ekstremum w każdym z punktów stacjonarnych, badamy znak hesjanu w każdym z tych punktów.
Pochodne cząstkowe drugiego rzędu funkcji są równe:
W punkcie hesjan jest równy
Ponieważ więc wnioskujemy, że funkcja nie ma ekstremum w punkcie
W punkcie hesjan jest równy
Ponieważ więc wnioskujemy, że funkcja ma ekstremum w punkcie Ponieważ więc jest to minimum.
Ostatecznie widzimy, że badana funkcja ma minimum lokalne w punkcie i jest to jej jedyne ekstremum.
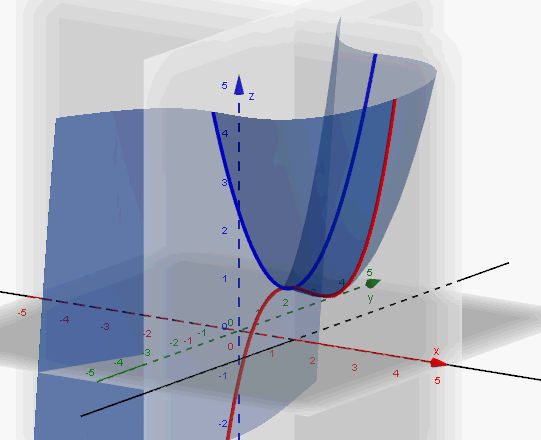
Rysunek poniżej ilustruje zachowanie funkcji w otoczeniu punktu , w którym ekstremum nie występuje. Brak ekstremum można na nim dodatkowo stwierdzić wizualnie, przyglądając się krzywym wyciętym z wykresu funkcji przez dwie płaszczyzny pionowe równoległe do płaszczyn układu współrzędnych.
[Egz] Zadanie 5
Wyznacz punkty stacjonarne funkcji Następnie zbadaj, w których spośród nich funkcja ma ekstrema i określ rodzaj tych ekstremów.
Punkty stacjonarne:
Funkcja ma minimum lokalne w punkcie i maksimum lokalne w punkcie
W pozostałych dwóch punkach stacjonarnych funkcja nie ma ekstremów.
Obliczamy pochodne cząstkowe:
Rozwiązujemy uklad równań
Wyznaczamy z drugiego równania i podstawiamy do pierwszego równania:
Otrzymujemy po przekształceniach równanie dwukwadratowe:
Podstawiamy i otrzymujemy równanie
Jego rozwiązaniami są
Otrzymujemy stąd następujące rozwiązania równania
i odpowiadające im wartości z zależności
Ostatecznie widzimy, że funkcja ma cztery punkty stacjonarne:
Badamy istnienie ekstremum w każdym z punktów dla
Pochodne cząstkowe drugiego rzędu funkcji są równe:
Wyznaczamy hesjan jako funkcję zmiennych W ten sposób łatwiej będzie nam badać jego znak w każdym z otrzymanych punktów stacjonarnych.
Z otrzymanej postaci widzimy, że i
Zatem spośród punktów stacjonarnych możemy od razu wyeliminować punkty i – hesjan jest w tych punktach ujemny.
W punktach i hesjan jest dodatni, zatem funkcja ma w tych punktach ekstrema.
Ponieważ więc oraz
Wnioskujemy ostatecznie, że funkcja ma minimum lokalne w punkcie i maksimum lokalne w punkcie
[Egz] Zadanie 6
Niech Wyznacz punkty stacjonarne funkcji , leżące w I ćwiartce układu a więc o obu współrzędnych dodatnich. Następnie zbadaj istnienie ekstremów funkcji w tych punktach i określ ich rodzaj.
W pierwszej ćwiartce istnieje jeden punkt stacjonarny: Funkcja ma w tym punkcie maksimum lokalne.
Obliczamy pochodne cząstkowe:
Rozwiązujemy uklad równań
Ponieważ punktów stacjonarnych szukamy tylko w I ćwiartce, więc interesują nas tylko takie rozwiązania, dla których oraz Biorąc pod uwagę to ograniczenie, możemy ostatni układ równań równoważnie przepisać jako
czyli
Rozwiązaniem ostatniego układu jest
Widzimy, że jedynym punktem stacjonarnym funkcji leżącym w I ćwiartce jest Zbadamy istnienie ekstremum naszej funkcji w tym punkcie.
Pochodne cząstkowe drugiego rzędu funkcji są równe:
W punkcie hesjan jest równy
Widzimy, że oraz
Wobec tego funkcja ma w badanym punkcie maksimum lokalne.