First, it is crucial for you to understand the method of characteristics for solving simple quasilinear equations without shock waves. Let us focus on Problem 7 from the 1st list, i.e. semi-linear equations. Suppose we would like to solve something similar, say

$$ \begin{cases} u_t + x t \, u_x = t(1+u^2), & t>0, \quad x\in\mathbb{R} \\ u(x,0)=\frac{x^2}{1+x^2}, & x\in\mathbb{R}. \end{cases} $$ So that $c(x,t) = x t$, that is the speed of wave propagation increases with $x$ and $t$. Note that it is negative for $x<0$. Moreover, the source term $t(1+u^2)$ increases both with time and the concentration. In the method of characteristics you have to form a system of ODEs (and understand how it arises)

$$ \begin{cases} X' = t X, & X(0) = \xi, \\ U' = t(1+U^2), & U(0) \stackrel{df}{=} u(X(0),0) = u(\xi, 0) = \frac{\xi^2}{1+\xi^2}. \\ \end{cases} $$

Remember that $\xi$ denotes the point at which the characteristic intersects the $t=0$ axis. It enumerates every member from the characteristic family. These equations usually have to be solved simultaneously however, in this simple example we can start with finding $X$. Since this is a simple ODE we immediately find out that

$$ X(t) = \xi e^{\frac{1}{2}t^2}, $$

and from here it is useful to find $\xi$, i.e.

$$ \xi(x,t) = x e^{-\frac{1}{2}t^2}. $$

Note that $\xi(x,t)$ is a $x$-coordinate of a point of intersection with $t = 0$ of a unique characteristic passing through $(x,t)$ (this is very important). A simple drawing of characteristics looks like this:

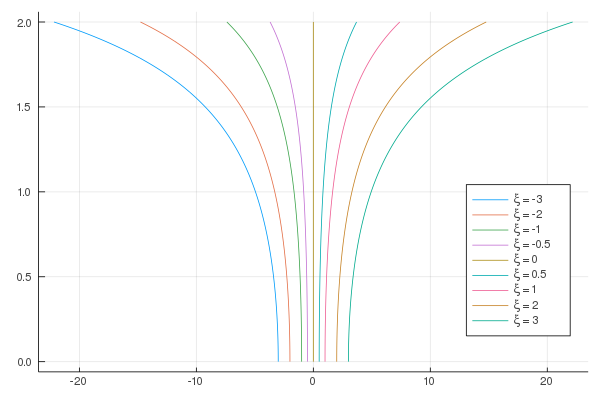
Knowing that we can proceed to solving for $U$, that is

$$ \frac{U'}{1+U^2} = t \quad \rightarrow \quad U(t) = \tan \left( \frac{1}{2} t^2 + C\right), $$

where the integration constant can be determined from the initial condition, that is

$$ \frac{\xi^2}{1+\xi^2} = U(0) = \tan C \quad \rightarrow \quad C = \arctan \frac{\xi^2}{1+\xi^2}. $$

Now, we know everything. We can combing the two above solutions with the definition of $U$ and write

$$ u(x,t) = U(t, \xi(x,t)) = \tan \left( \frac{1}{2} t^2 + \arctan \frac{x^2 e^{-t^2}}{1+x^2 e^{-t^2}}\right), $$

where in the first equality we have clearly indicated that $U$ depends also on $\xi$. This is a highly artificial example, however, it outlines all the necessary steps used in solving semi-linear equations.

Now, in Problem 9 you proceed similarly. However, there is an important difference: you solve your problem on a quarter-plane $x>0$ and $t>0$. So that, you have two sets on which the conditions are given: $t = 0$ (initial) and $x = 0$ (boundary). The most important point is to remember that if you know characteristics, you know everything. Now, since your data is given on a different axes, you have to separate the characteristics according which axis it intersects first. This is clear from the following picture

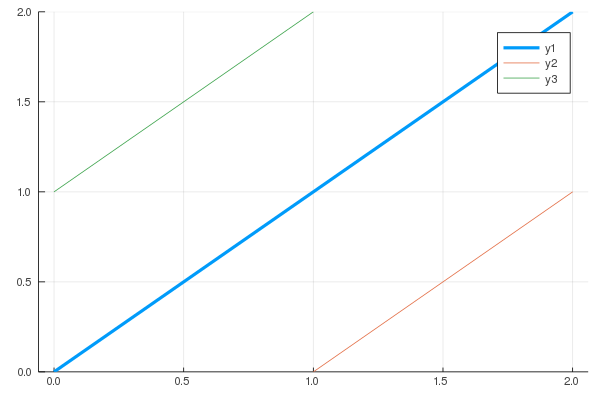
We can see that the thick line is a characteristic that separates two families of them: one intersecting the $t=0$ while the other $x = 0$. Solving the characteristic equation for $X$ will help you to determine which characteristics belong to which family. Remember that for each family you have different integration constants (in equation for $X$). The red family is the one you know very well - it is an initial value problem and you solve it as usual with determining $\xi$. However, the green family does not intersect $t = 0$ but rather $x = 0$. And it is very useful to determine the integration constant for which $ x = 0 $ when $t = \tau$ (since there the condition is given). Call it $\tau$. For the simple example above, the characteristics have the linear form

$$ X(t) = x-\tau. $$

Compare this with the initial value problem for which you had $ t = 0 $ for $x = \xi$. Finally, the whole Problem 9 can be solved by separating the characteristics as above and integrating the equation for $U$ using different condition for each family.

In Problem 10 we have quasilinear equations, however, the overall method stays the same. For example, the first problem gives us the following characteristic equations

$$ \begin{cases} X' = \ln U, & X(0) = \xi, \\ U' = 0, & U(0) = e^{\xi}. \end{cases} $$

Note that now we cannot first solve for $X$ since we do not know $U$. But from the second equation we obtain $U(t) = \text{const.} = \exp(\xi)$. Then, $X' = \ln \exp(\xi) = \xi$ and hence

$$ X(t) = (1+t)\xi, $$

and from here $\xi(x,t) = x/(1+t)$ whence, $u(x,t) = U(t,\xi(x,t)) = \exp(x/(1+t))$.

Finally, Problem 11 combines everything of the above into one equation. You should not have any problems in solving it. Remember, it is very useful to draw everything.