

Statystyka Matematyczna
Powtórka z rachunku prawdopodobieństwa
Piotr Sobczyk
PWr
Zasady zaliczania ćwiczeń
- Jedno kolokwium (6 zadań po 5 punktów)
- Aktywność - do 4 punktów
- Zaliczenie od 15
- Maksymalna liczba nieobecności to 30\% czyli 2 zajęcia
- Moja strona: im.pwr.edu.pl/~sobczyk
Zmienna losowa
- Wartość zależna od wyniku eksperymentu
- Zmienna przyjmująca wartości numeryczne, zależna od wyniku zdarzenia losowego
- Funkcja przypisująca zdarzeniom elementarnym liczby (wiki)
Zmienna losowa dyskretna
- Zbiór możliwych wyników jest albo skończony albo przeliczalny (np. liczby naturalne)
- Jak prawdodpobne jest uzyskanie danego wyniku? Opisujemy to przez funkcja prawdopodobieństwa \[p_X(x) - P(X=x)\]
- Prawdopodobieństwo, że dostaniemy jakiś, dowolny, wynik wynosi 1: \(\sum_x p_X(x) =1\) -
Zmienna losowa dyskretna - przykład
Losujemy jedną rodzinę z całej Polski. Wartości zmiennej losowej X odpowiadają liczbie dzieci w tej rodzinie. Jakie są możliwe rezultaty? Jak policzyć prawdopodobieństwo wystąpienia rodziny z trójką dzieci?
Zatwierdź i porównaj WyczyśćZmienna losowa ciągła
- Losujemy człowieka z pewnej populacji (to nasze zdarzenie losowe)
- Wartości zmiennej losowej X odpowiadają wzrostowi wylosowanej osoby.
- W tym wypadku liczba możliwych wyników nie jest dyskretna a przyjmuje dowolną wartość rzeczywistą
- Rozkłady ciągły opisujemy przez funkcję zwaną dystrybuantą (np. \[P(X \leq 1.80) = 0.73\]) lub funckję gęstości
Zmienna losowa ciągła \(X\)
- Funkcja gęstości \(f_X(x)\)
- Dystrybuanta \(F_X(t) := P(X\leq t) = \int_{-\infty}^{t} f_X(x) dx\)
- \(1 = P(X \leq \infty) = \int_{-\infty}^{\infty} f_X(x) dx\)
Definicja wartości oczekiwanej
- Mamy zmienną losową X o wartościach w zbiorze \(\{x_1, x_2, ... \}\)
- \[\mu_{x} = E(X) = \sum_{i=1} x_i P(X= p_i) = \sum_{i=1} x_i p_i\]
- \[Var(X) = \sum_{i=1} (x_i-\mu_x)^2 P(X=x_i) = \sum_{i=1} x_i^2 p_i - \mu_x^2\]
- P-d. Rzut monetą, X=1, gdy orzeł, X=0, gdy reszka. E(X) = ? , Var(X) = ?
Przykład - rybie kręgi
Jaka jest wartość oczekiwana zmiennej losowej Y, mierzącej liczbę kręgów w ogonie w populacji ryb z gatunku, Cottus rotheus, jeśli jej rozkład jest następujący.
| Liczba kręgów | Procent ryb |
|---|---|
| 20 | 3 |
| 21 | 51 |
| 22 | 40 |
| 23 | 6 |
| Łącznie | 100 |
- 21.49
- 21.00
- 21.32
Korzystamy ze wzoru:
E(Y) = 20 * P(Y=20) + 21 * P(Y=21) + 22 * P(Y=22) + 23 * P(Y=23) = 20 * 0.03 + 21 * 0.51 + 22 * 0.40 + 23 * 0.06 = 21.49.
Przykład - rybie kręgi
Jakie jest odchylenie standardowe zmiennej losowej Y, mierzącej liczbę kręgów w ogonie w populacji ryb z gatunku, Cottus rotheus, jeśli jej rozkład jest następujący.
| Liczba kręgów | Procent ryb |
|---|---|
| 20 | 3 |
| 21 | 51 |
| 22 | 40 |
| 23 | 6 |
| Łącznie | 100 |
- 0.4299
- 0.6557
- 0.49
Należy skorzystać ze wzoru na wariancję.
\[Var(Y) = (20-21.49)^2 * P(Y=20) + (21-21.49)^2 * P(Y=21) +\] \[(22-21.49)^2 P(Y=22) + (23-21.49)^2 P(Y=23) \sim 0.4299\]
Odchylenie standardowe jest pierwiastkiem z wariancji.
Definicja wartości oczekiwanej
- Mamy zmienną losową ciągłą X o funckji gęstości \(f_X\)
- \[\mu_{X} = E(X) = \int_{-\infty}^{\infty} x f_X(x) dx\]
- \[Var(X) = E (X - E(X))^2 = \int_{-\infty}^{\infty} (x-E(X))^2 f_X(x) dx= \int_{-\infty}^{\infty} x^2 f_X(x) dx - (E(X))^2\]
- P-d. Długość kroku losowo wybranego studenta PWr
Przykład - rozkład jednostajny
Załóżmy, że czas oczekiwania, liczony w minutach, na przyjazd autobusu ma rozkład jednostajny na przedziale [0, 15].(podaj trzy cyfry znaczące)
- Ile wynosi wartość oczekiwana?
- Ile wynosi odchylenie standardowe?
- 7.5
- 4.33
Funkcja gęstości rozkładu jednostajnego to \(f_X(x)= \frac{1}{A-B} 1_{x \in [A,B]}\), gdzie A,B to granice przedziału, a \(1\) to funkcja indykatorowa. Skorzystaj z definicji.
Przykład - rozkład wykładniczy
Czas oczekiwania (w minutach) na zgłoszenie konsultanta w call center ma rozkład wykładniczy w parametrem \(\lambda=\frac{1}{5}\)
- Ile wynosi oczekiwany czas na zgłoszenie się konsultanta?
- Jakie jest prawdopodobieństwo, że będziemy czekać krócej niż minutę?
- Jakie jest prawdopodobieństwo, że będziemy czekać dłużej niż 10 minut?
- 5
- 0.1812692
- 0.1353353
Funkcja gęstości rozkladu wykładniczego to \(f_X(x)= \lambda e^{-\lambda x}\). Skorzystaj z definicji. Przedstaw prawdopodobieństwa w postaci całek np. \(P(X>10) = \int_{10}^{\infty} f(x) dx\)
Własności wartości oczekiwanej i wariancji
E(aX+b)=
- a E(X) +b
Var(aX+b) =
- \(a^2\) Var(X)
E(X+Y)=
- EX+EY
Niezależność zmiennych losowych
Jeżeli zmienne losowe X,Y są niezależne, to \[P(X \in A, Y \in B) = P(X \in A) P(X \in B)\] dla dowolnych zbiorów A i B.
Przykład 1
X - Kto wygra nagrodę Nobla z fizyki, A - osoby o nazwisku na literę A
Y - Kto wygra program Top Model, B - osoby o nazwisku na literę B
Przykład 2
Wybieramy (losowo) liczbę dwucyfrową
X:=liczba dziesiątek, Y:=liczba jedności,
\(A=\{1, 2\}\), \(B=\{3, 4, 5\}\).
Niezależne zmienne losowe
Jeśli zmienne losowe X, Y są niezależne, to \[E(X \cdot Y) = E(X) \cdot E(Y)\] oraz \[Var(X + Y) = Var(X) + Var(Y)\] Jeśli \(Var(X)=3\) i \(Var(Y)=2\), to
- Var(X-Y+2) =
- Var(X+X) =
- 5
- 12
X-Y = X + (-Y). Jak wariancja zmienia się po dodaniu stałej?
Schemat Bernoulliego:
- n niezależnych powtórzeń tego samego eksperymentu
- dwa możliwe wyniki w każdej próbie - ,,sukces" i ,,porażka" (np. Orzeł i Reszka, albo 1 i 0)
- w każdej próbie p-stwo sukcesu wynosi p
Rozkład dwumianowy:
Y = łączna liczba sukcesów w schemacie Bernoulliego
Rozkład dwumianowy
Wzór na rozkład dwumianowy \[P(Y=k) = {n \choose k} p^k (1-p)^{n-k}\] \[{n \choose k} = \frac{n!}{k! (n-k)!}\]
Możliwe wyniki to k=1,2,3,...n
\[\mu_Y = E(Y) = n \cdot p\] \[Var(X) = n \cdot p \cdot (1-p)\]
Przykład
Anita, Beata i Celina rzucają trzema symetrycznymi monetami. Uzyskaną przez nie łączną liczbę orłów oznaczamy przez zmienną losową Y. Jakie możemy uzyskać wyniki i jak są one prawdopodobne?
- \(P(Y=0)=\)
- \(P(Y=1)=\)
- \(P(Y=2)=\)
- \(P(Y=3)=\)
- 0.125
- 0.375
- 0.375
- 0.125
Skorzystaj ze wzoru na rozkład dwumianowy. Pamiętaj, że \(p=\frac{1}{2}\).
Schemat Bernoulliego
Anita, Beata i Celina rzucają symetrycznymi monetami. Zliczamy liczbę wyrzuconych orłów. Swoje rzuty powtarzają one 10-krotnie. Uzyskane wyniki nie muszą się idealnie zgadzać z teoretycznymi wartościami
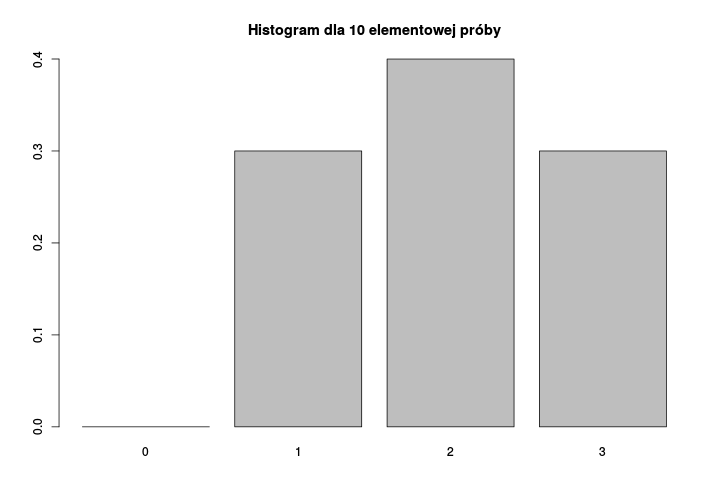
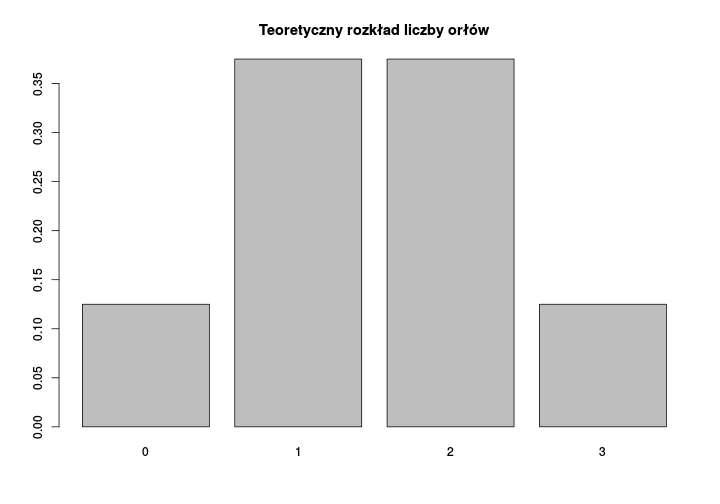
Schemat Bernoulliego
Im więcej rzutów wykonają Anita, Beata i Celina, tym częstości uzyskanych orłów będą bliższe wartościom teoretycznym. Jest to przykład działania Centralnego Twierdzenia Granicznego (CTG).
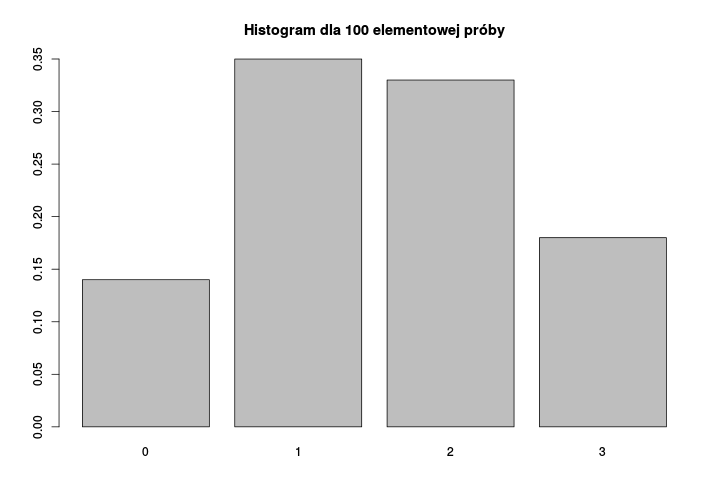
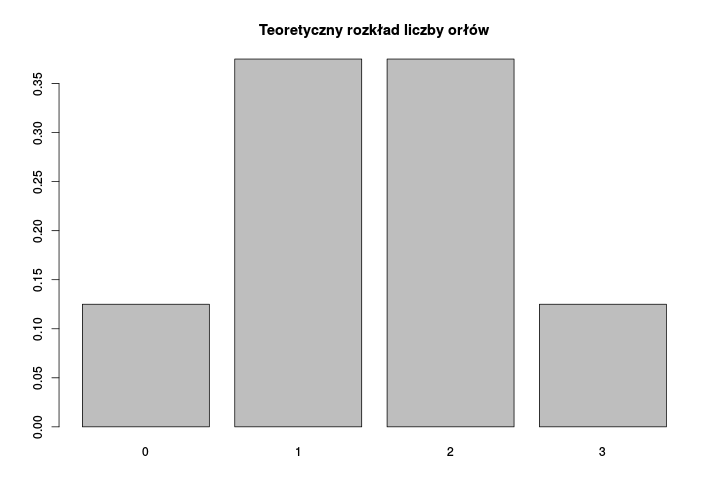
Przykład - kontynuacja
Jeden na ośmiu dorosłych mężczyzn ma podniesiony poziom cholesterolu. Losowo wybieramy 10 mężczyzn z populacji.
- Jakie jest p-stwo, że (dokładnie) 2 spośród nich ma podniesiony poziom cholesterolu ?
- Jakie jest p-stwo, że co najmniej jeden z nich ma podniesiony poziom cholesterolu?
- Ilu, średnio, mężczyzn na dziesięciu ma podwyższony poziom cholesterolu?
- 0.2416
- 0.3611022
- 1.25
Czy mamy do czynienia ze schematem Bernoulliego? Ile wynosi \(p\)? Pamiętaj, że \(P(X \leq x) = \sum_{t=0}^x P(X=t)\).